개발자는 기록이 답이다
Prefix를 빠르게 검색할때, MySQL에서 Index가 있다면 Java에서는 트라이(Trie)를 사용하자. 본문
Prefix를 빠르게 검색할때, MySQL에서 Index가 있다면 Java에서는 트라이(Trie)를 사용하자.
slow-walker 2024. 6. 29. 17:31

우리가 구글에서 검색할 때, '문자여'만 입력해도 다음에 나올 단어들이 자동완성처럼 제안되는 것을 흔히 볼 수 있습니다. 이는 Prefix 검색 덕분입니다. 그렇다면 데이터베이스에서는 어떻게 이러한 Prefix 검색을 빠르게 처리할 수 있을까요?
📌 MySQL에서 인덱스 사용
데이터베이스에서 특정 데이터를 빠르게 찾아오기 위해 인덱스(Index)를 사용합니다. 인덱스는 디스크 파일에 저장된 데이터를 빠르게 검색할 수 있게 도와줍니다. MySQL에서의 인덱스는 주로 B+ Tree 자료구조를 기반으로 구성됩니다.
B+ 트리는 B-Tree에서 파생된 개념입니다. B-Tree는 트리 구조의 최상위에 하나의 루트 노드(Root Node)가 존재하고, 그 하위에 자식 노드가 붙어있는 형태입니다. 트리 구조의 가장 하위에 있는 노드를 리프 노드(Leaf Node)라고 하며, 중간 노드를 브랜치 노드(Branch Node)라고 부릅니다.
데이터베이스에서 인덱스와 실제 데이터는 따로 관리되는데, 인덱스의 리프 노드는 항상 실제 데이터 레코드를 찾아가기 위한 주소값을 가지고 있습니다.
Real Mysql 1권 p.220

📌 Prefix 기반 문자열 검색
이러한 인덱스를 활용하면 주로 문자열 검색에서 Prefix(접두사) 기반으로 데이터를 빠르게 찾는데 용이합니다.
예를 들어, 아래와 같은 패턴을 가진 문자열을 검색할 때
select *
from book
where title like 'abc%';
해당 쿼리는 'abc'로 시작하는 모든 문자열을 빠르게 찾아낼 수 있습니다. 이는 B+ 트리의 효율적인 구조 덕분입니다.
그렇다면 자바에서 문자열 Prefix 검색을 할때는 어떤 자료구조를 사용해야할까요?
바로 Trie 구조입니다.
📌 Trie 구조
트라이는 검색 트리의 일종으로, 키가 문자열인 동적 배열 또는 연관 배열을 저장하는 정렬된 트리 자료구조입니다. 트라이는 1959년에 처음 공개되었으며, 검색을 뜻하는 ‘retrieval’의 중간 음절에서 용어를 따왔습니다. 트라이는 트리와 유사하지만 전형적인 다진 트리(m-ary Tree)의 형태를 띱니다.
트라이는 각각의 문자 단위로 색인을 구축한 것과 유사합니다. 예를 들어, 단어 'apple'을 찾는다고 가정해보겠습니다. 트라이 탐색을 하면 다섯 번만에 'apple' 문자열의 존재 여부를 파악할 수 있습니다. 이는 문자열의 길이만큼만 탐색하면 되기 때문입니다.
이처럼 간편하고 효율적으로 탐색할 수 있기 때문에, 자연어 처리 분야에서는 형태소 분석기 등에서 분석 패턴을 트라이로 만들어두고 자연어 문자에 대해 패턴을 찾아 처리하는 등의 형태로도 활용되고 있습니다.
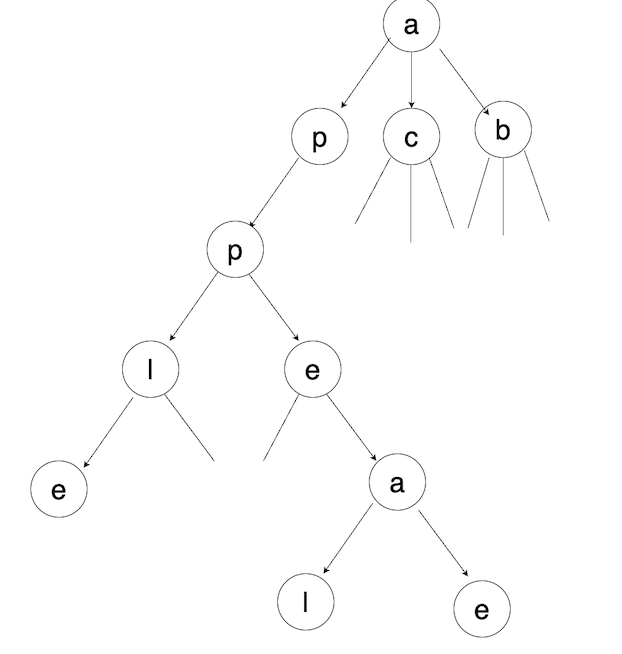
위의 그림은 'apple', 'appear', 'appeal' 등으로 구성된 Trie의 예제입니다.
여기서 만약 'apple'을 찾는다면 a -> p -> 순으로 문자별 일치하는 노드를 찾아 내려가고, 그 다음은 l 노드를 찾아가면 됩니다. 만약 'applear'을 찾는다면 e노드를 찾아가면 됩니다.
이처럼 트라이에서는 각 문자열의 길이만큼만 탐색하면 원하는 결과를 찾을 수 있습니다.
트라이는 문자열을 위한 트리 형태이기 때문에 사실상 문자의 개수만큼 자식이 있어 상당히 많은 자식 노드를 갖고 있는 트리인것을 알 수 있습니다.
📌 Trie 구현
https://leetcode.com/problems/implement-trie-prefix-tree/
트라이 노드를 의미하는 클래스를 선언해보겠습니다. 위의 리트코드 문제를 통해 트라이 자료구조를 구현해보겠습니다.
TrieNode라는 클래스로 각각의 노드를 만들고, 자식 노드는 children이라는 멤버 변수에 묶이는 형태가 될 것입니다.
// 트라이의 노드
class TrieNode {
// 단어 완성 여부
boolean word;
// 트라이의 자식 노드들
TrieNode[] children;
public TrieNode() {
children = new TrieNode[26];
word = false;
}
}
다음으로, 트라이 연산을 구현할 별도의 클래스인 Trie를 선언하겠습니다.
가장 먼저 삽입 메소드 부터 구현해보자면,
처음 Trie클래스를 생성하면 루트 노드로 별도 선언한 TrieNode 클래스를 멤버변수로 갖게 되고,
노드 추가 시 루트부터 자식 노드가 점점 깊어지면서 문자 단위의 다진 트리 형태가 됩니다.
class Trie {
TrieNode root;
public Trie() {
root = new TrieNode();
}
public void insert(String word) {
// 루트 노드부터 시작
TrieNode cur = root;
// 단어의 문자를 차례대로 순회합니다.
for(char c : word.toCharArray()) {
// 해당 문자의 자식 노드가 존재하지 않으면 신규 트라이 노드 생성
// 'a'가 인덱스 0, 'z'는 인덱스 25가 됩니다.
if (cur.children[c - 'a'] == null) {
// 루트 추가 시 자식 노드가 점점 깊어지면서 문자 단위의 다진 트리 형태
cur.children[c- 'a'] = new TrieNode();
}
// 자식 노드를 현재 노드로 교체합니다.
cur = cur.children[c-'a'];
}
// 단어의 마지막 노드에 도달하면 word 플래그를 true로 설정하여 단어의 끝임을 표시합니다.
cur.word = true;
}
}
자식 노드의 인덱스를 정할 때 유의할 점이 있습니다.
자바는 문자에서 문자를 빼면 아스키 코드 값의 차이를 리턴합니다.
정확히는 유니코드의 값을 리턴하는데, 알파벳의 경우 유니코드가 아스키 코드와 동일하기 때문에 문제의 제약 조건에 따라 소문자 알파벳만 저장하는 경우 아스키 코드 값의 차이가 리턴됩니다.
$ 'a' - 'a'
0
$ 'f' - 'a'
5
$ 'z' - 'a'
25
이렇게 하면 'a'를 0번 인덱스로 하고, 'z'를 25번 인덱스로 지정해 저장할 수 있습니다.
알파벳 소문자만 이루어진 것을 가정한다면 자식 노드의 개수가 26개이기 때문에 딱 들어맞게 됩니다.
이렇게 하면 입력값이 apple인 경우, 삽입 코드를 아래처럼 사용할 수 있습니다.
Trie t = new Trie();
t.insert("apple");
그러면 아래와 같은 형태를 띄게 되는데, 이 그림에서 트라이는 다음 문자를 키로 하는 자식 노드 형태로, 점점 깊어지면서 또한 각각의 노드는 word값만 갖게 됩니다. 이 값은 단어가 모두 완성됐을 때만 true가 됩니다. 즉 apple의 경우 단어가 모두 완성되는데 e에 이르러서야 true로 설정됩니다.
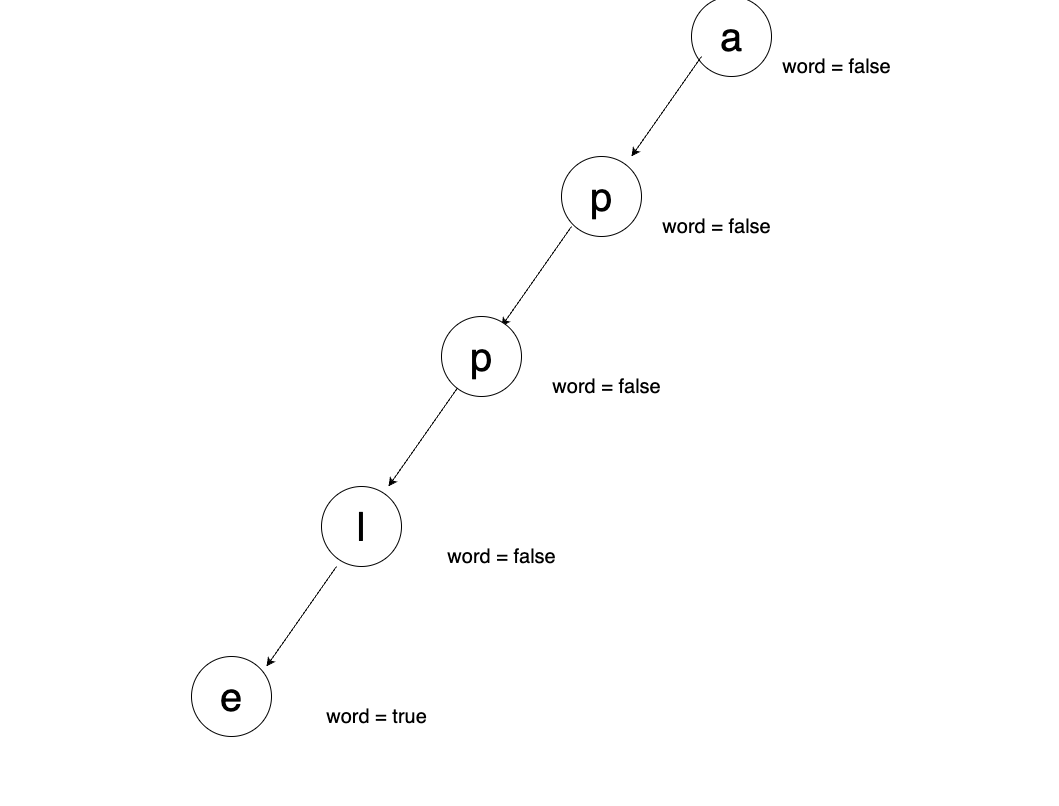
디버깅을 통해 알아보면 아래와 같습니다.
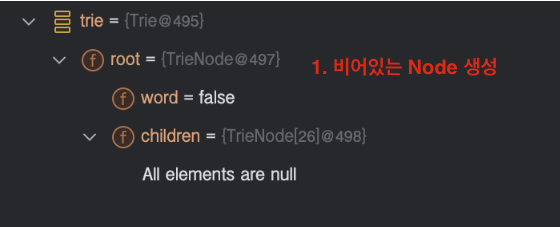
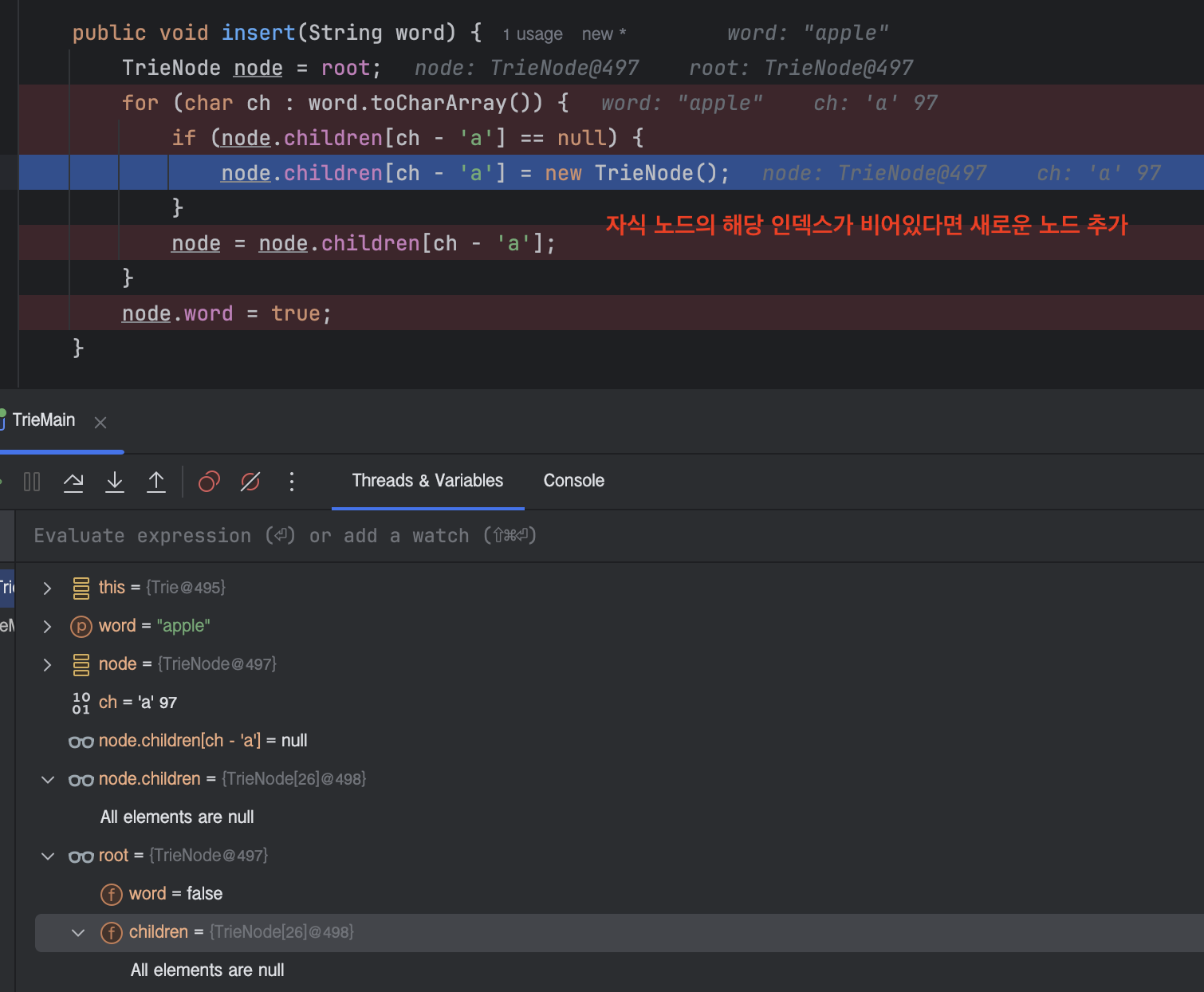
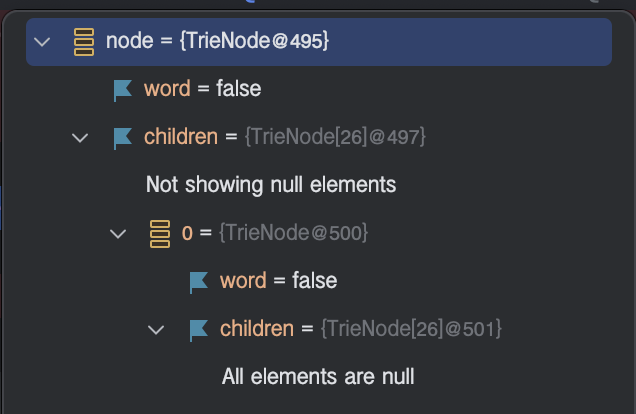
배열 중 각 알파벳이 해당하는 인덱스에 새로운 노드를 추가하고, 해당 노드로 현재 노드를 교체하는 것을 반복하다보면 아래처럼 만들어집니다.
node = {TrieNode@495}
word = false
children = {TrieNode[26]@497}
0 = {TrieNode@500}
word = false
children = {TrieNode[26]@501}
15 = {TrieNode@502}
word = false
children = {TrieNode[26]@503}
15 = {TrieNode@504}
word = false
children = {TrieNode[26]@505}
11 = {TrieNode@506}
word = false
children = {TrieNode[26]@507}
4 = {TrieNode@508}
word = true
children = {TrieNode[26]@509}
만약 apple외에 appear, appeal같은 단어를 추가로 삽입한다면 동일하게 삽입 메소드를 사용하면 됩니다.
t.insert("appear");
t.insert("appeal");
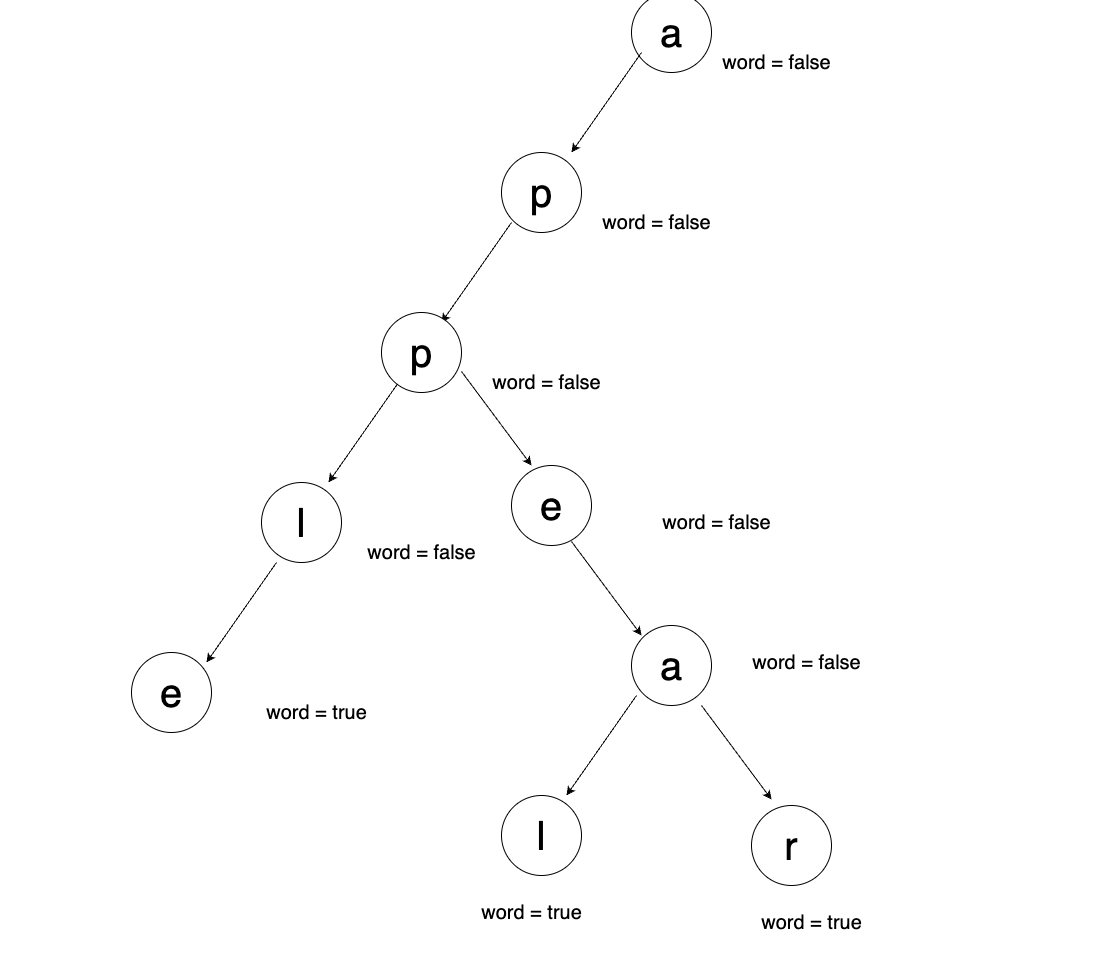
마찬가지로 트라이를 구성하는 다진 트리는 아래 그림같은 형태가 되고, 이 그림에서 트라이는 app까지 같은 문자는 같은 자식을 타고 내려다가다가, 달라지는 문자부터 서로 다른 노드로 분기됩니다. 마지막에 appeal과 appear가 완성되는 l과 r 노드가 각각 word = true로 설정되는데, 이게 트라이 구조의 삽입의 기본 원리입니다.
이어서 이 값이 존재하는지 확인하기 위해 search()와 startwith()메소드를 만들어보겠습니다.
search()는 단어가 존재하는지 여부를 ㅍ나별하는 것이고, startsWith()메소드는 해당 문자열로 시작하는 단어가 존재하는지 여부를 판별합니다. 즉 둘 다 동일하게 문자 단위로 계속 깊이 탐색을 하고 startsWith()인 경우에만 마지막에 word가 true인지 확인하면 됩니다.
먼저 search() 코드입니다.
// 단어 존재 여부 판별
public boolean search(String word) {
// 루트부터 시작
TrieNode cur = root;
// 단어의 문자를 차례대로 반복하며 자식 노드 구성
for (char c : word.toCharArray()) {
// 현재 문자가 가리키는 자식 노드가 존재하지 않으면 false 리턴
if (cur.children[c - 'a'] == null) return false;
// 자식 노드를 현재노드로 교체
cur = cur.children[c - 'a'];
}
// 탐색이 종료된 후 단어 완성 여부를 리턴
// 완성된 단어가 아니라면 문자는 모두 매칭이 되어도 단어 완성 여부는 false일 수 있음
return cur.word == true;
}
문자열에서 문자를 하나씩 for 반복문으로 순회하면서 깊이 기반으로 자식 노들르 계속 타고 내려갑니다.
그리고 마지막에 cur.word의 true 여부를 리턴합니다. 만약 단어가 완성된 트라이라면 true로 되어 있을 것이고, 이때 true가 리턴됩니다.
다음올 startsWith()메소드입니다. search()와 완전히 동일하되 맨 마지막에 cur.word의 true여부를 확인하는 부분만 제외하면 됩니다.
// 문자열로 시작 단어 존재 여부 판별
public boolean startsWith(String prefix) {
// 루트부터 시작
TrieNode cur = root;
// 단어의 문자를 차례대로 반복하며 자식 노드 구성
for (char c : prefix.toCharArray()) {
// 현재 문자가 가리키는 자식 노드가 존재하지 않으면 false 리턴
if (cur.children[c - 'a'] == null) return false;
// 자식 노드를 현재 노드로 교체
cur = cur.children[c - 'a'];
}
// 탐색이 종료되면 항상 true 리턴, 시작 여부만 판별하면 되므로 단어 완성 여부가 false여도 관계없음
return true;
}
완성된 전체 코드는 아래와 같습니다. 이름만 봐서는 복잡하고 어려운 알고리즘 같지만, 직접 구현해보면 생각만큼 어렵지 않은 것을 알 수 있고 문자 단위로 자식 노드를 만들어 탐색한다는 개념만 확실히 이해하면 됩니다.
class TrieNode {
boolean word;
TrieNode[] children;
public TrieNode() {
children = new TrieNode[26];
word = false;
}
}
class Trie {
TrieNode root;
public Trie() {
root = new TrieNode();
}
public void insert(String word) {
// 루트 노드부터 시작
TrieNode cur = root;
// 단어의 문자를 차례대로 반복하면서 자식 노드 구성
for(char c : word.toCharArray()) {
// 해당 문자의 자식 노드가 존재하지 않으면 신규 트라이 노드 생성
// 'a'가 인덱스 0, 'z'는 인덱스 25가 된다.
if (cur.children[c - 'a'] == null) {
// 루트 추가 시 자식 노드가 점점 깊어지면서 문자 단위의 다진 트리 형태
cur.children[c- 'a'] = new TrieNode();
}
// 자식 노드를 현재 노드로 교체
cur = cur.children[c-'a'];
}
// 단어가 원성된 후이므로 현재 노드는 단어 완성 여부에 true설정
cur.word = true;
}
// 단어 존재 여부 판별
public boolean search(String word) {
// 루트부터 시작
TrieNode cur = root;
// 단어의 문자를 차례대로 반복하며 자식 노드 구성
for (char c : word.toCharArray()) {
// 자식 노드가 존재하지 않으면 false 리턴
if (cur.children[c - 'a'] == null) return false;
// 자식 노드를 현재노드로 교체
cur = cur.children[c - 'a'];
}
// 탐색이 종료된 후 단어 완성 여부를 리턴
// 완성된 단어가 아니라면 문자는 모두 매칭이 되어도 단어 완성 여부는 false일 수 있음
return cur.word == true;
}
// 문자열로 시작 단어 존재 여부 판별
public boolean startsWith(String prefix) {
// 루트부터 시작
TrieNode cur = root;
// 단어의 문자를 차례대로 반복하며 자식 노드 구성
for (char c : prefix.toCharArray()) {
// 자식 노드가 존재하지 않으면 false 리턴
if (cur.children[c - 'a'] == null) return false;
// 자식 노드를 현재 노드로 교체
cur = cur.children[c - 'a'];
}
// 탐색이 종료되면 항상 true 리턴, 시작 여부만 판별하면 되므로 단어 완서 ㅇ여부가 false여도 관계없음
return true;
}
}'언어 > Java' 카테고리의 다른 글
| Exception Wrapping vs Rethrowing (0) | 2024.03.25 |
|---|---|
| 왜 자바 직렬화는 Serializable 인터페이스가 있어야할까? (0) | 2024.01.30 |
| Executor, ExecutorService, Executors 동작원리 ( + ThreadPoolExecutor 디버깅) (1) | 2024.01.26 |
| HashMap이 동작하는 원리를 파헤쳐보자 + putVal메소드 디버깅 (0) | 2024.01.21 |
| [Java] String 덧셈 연산의 컴파일 최적화에 대해 알아보자 (0) | 2024.01.12 |



