Notice
Recent Posts
Recent Comments
Link
개발자는 기록이 답이다
자바(Java) 알고리즘 문제풀이 입문: 코딩테스트 대비(DFS/BFS_Tree 말단노드까지의 까장 짧은 경로) 본문
알고리즘/인프런 - Java알고리즘 입문
자바(Java) 알고리즘 문제풀이 입문: 코딩테스트 대비(DFS/BFS_Tree 말단노드까지의 까장 짧은 경로)
slow-walker 2023. 9. 28. 04:03
9. 10. Tree 말단노드까지의 까장 짧은 경로(DFS/BFS)
루트노드에서 말단 노드까지 가는데 이동하는 횟수를 즉 간선(에지)의 개수를 구하라

이런 최단 거리 문제는 BFS로 풀어야 맞습니다. 하지만 배우기 위해 DFS로는 어떻게 풀어야하는지 알아보겠습니다.
DFS는 제약이 있습니다. 3번 노드에서 자식노드가 6번 노드로 하나만 있을 경우 풀기 어렵습니다.
정확하게 2개 자식노드가 있거나 아예 없어야 합니다. BFS에서는 레벨 탐색이라 상관없습니다.
DFS : Depth-First Search
0,1,2레벨이 있는데 한번만에 가는 1레벨은 말단 노드라면 3원소입니다.
레벨이 바로 문제에서 정의하는 이동 횟수(거처가는 간선의 횟수)를 말합니다.
말단 노드를 만났을때, 매개변수에 있는 root가 가르키는 노드의 레벨 값이 L입니다.
그때 루트가 가르키는가 말단 노드 일경우 L을 리턴해주면 그것이 바로 이동 거리입니다.
class Node {
int data;
Node lt, rt;
public Node(int val) {
data = val;
lt = rt = null;
}
}
public class Main {
Node root;
public int DFS(int L, Node root) { // root가 가르키는 말단 노드의 레벨값이 L
// 말단 노드일 경우
if (root.lt == null && root.rt == null) return L;
// 리턴 받은 값 중에 작은 값을 선택해야해서 min함수 사용
else return Math.min(DFS(L + 1, root.lt), DFS(L + 1, root.rt));
// 특정 노드를 만나면 왼쪽과 오른쪽으로 뻗는걸로 가정이 되어서 자식이 하나면 안된다.
}
public static void main(String[] args) {
Main tree = new Main();
tree.root = new Node(1);
tree.root.lt = new Node(2);
tree.root.rt = new Node(3);
tree.root.lt.lt = new Node(4);
tree.root.lt.rt = new Node(5);
System.out.println(tree.DFS(0, tree.root)); // 0번 레벨의 100번지
}
}
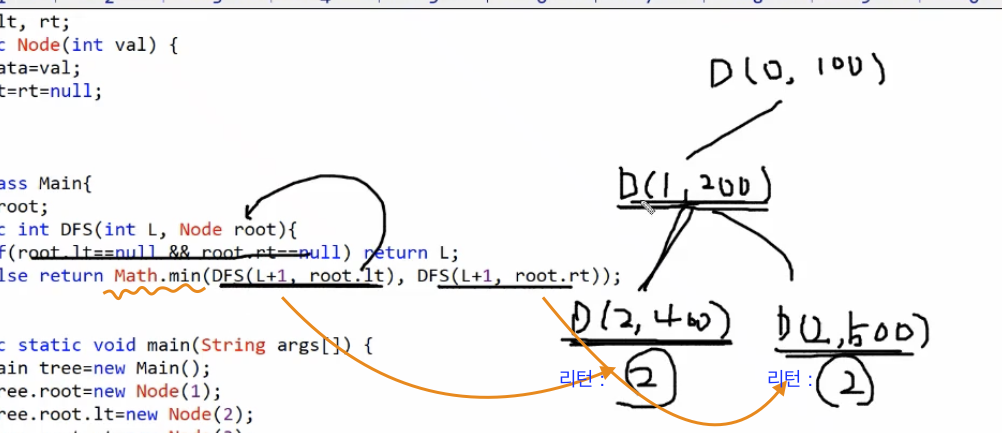
- 제일 처음 0번 레벨의 100번지가 호출된다
- else문으로 들어와서 레벨1의 200번지를 호출한다.
- 레벨 2의 400번지(lt) 와 레벨 2의 500번지(rt)는 자식노드가 null인 말단노드이기 때문에 레벨 2를 리턴한다.
- 왼쪽 노드와 오른쪽 노드의 리턴값 중의 최소값을 레벨 1의 200번지한테 리턴해준다.
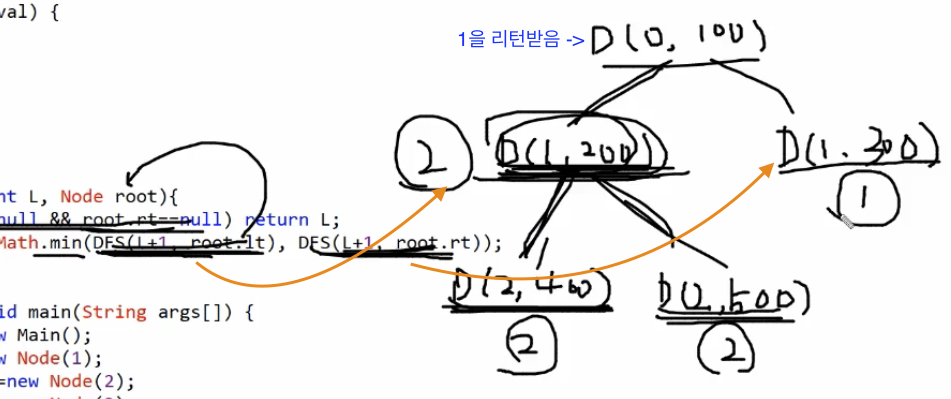
- 1레벨의 200번지에서 백에서 0레벨의 100번지에서 오른쪽 노드로 DFS재귀함수를 호출한다.
- 1레벨의 300번지는 말단노드이기 때문에 레벨 1을 리턴한다.
- 2를 리턴받은 1레벨의 200번지와 1를 리턴하는 1레벨의 300번지 중 최솟값인 1을 0레벨의 100번지로 리턴한다.
BFS : Breadth-First Search
BFS가 왜 최단 거리 문제에 효과적인 풀이 일까요?
레벨 탐색을 하다가 말단 노드가 발견됬을 경우, 그것이 최단 거리의 말단 노드입니다.
가장 짧은 것들부터 다 방문해보니까 최단 거리에 효과적입니다.
import java.util.LinkedList;
import java.util.Queue;
class Node {
int data;
Node lt,rt;
public Node(int val) {
data = val;
lt=rt=null;
}
}
public class Main {
Node root;
// 매개변수의 root는 레벨 탐색이라 100,200,300,400,500번지 순으로 들어갑니다
// 깊이 우선 탐색은 100번지, 200번지,400번지, 300번지 막 다닙니다.
public int BFS(Node root) {
Queue<Node> Q = new LinkedList<>();
Q.offer(root);
int L = 0;
// 비어있을때 거짓이 되서 반복문을 돌고, 비어있지 않으면 참이 됩니다
while (!Q.isEmpty()) {
int len = Q.size();
for (int i = 0; i < len ; i++) {
Node cur = Q.poll(); // 레벨에 있는 노드들 다 빼내기
if(cur.lt == null && cur.rt == null) return L; // 말단 노드일 경우
if (cur.lt != null) Q.offer(cur.lt);
if (cur.rt != null) Q.offer(cur.rt);
}
L++;
}
return 0;
}
public static void main(String[] args) {
Main tree = new Main();
tree.root = new Node(1);
tree.root.lt = new Node(2);
tree.root.rt = new Node(3);
tree.root.lt.lt = new Node(4);
tree.root.lt.rt = new Node(5);
System.out.println(tree.BFS(tree.root));
}
}'알고리즘 > 인프런 - Java알고리즘 입문' 카테고리의 다른 글
| 자바(Java) 알고리즘 문제풀이 입문: 코딩테스트 대비(Graph/DFS_경로탐색_인접행렬) (0) | 2023.09.28 |
|---|---|
| 자바(Java) 알고리즘 문제풀이 입문: 코딩테스트 대비(Graph_인접행렬) (0) | 2023.09.28 |
| 자바(Java) 알고리즘 문제풀이 입문: 코딩테스트 대비(BFS_송아지 찾기1) (0) | 2023.09.28 |
| 자바(Java) 알고리즘 문제풀이 입문: 코딩테스트 대비(BFS_이진트리 레벨탐색(BFS : Breadth-First Search)) (0) | 2023.09.28 |
| 자바(Java) 알고리즘 문제풀이 입문: 코딩테스트 대비(DFS_부분집합 구하기) (0) | 2023.09.28 |



